Hukum Newton 2

1. Jika ditarik dengan gaya yang sama mobil-mobilan yang massanya lebih besar (ada beban) percepatannya lebih kecil.

 

2. seorang anak mendorong meja ,berarti dia memberi gaya pada meja.

3. seorang anak menimba air dalem sumur, 

4. Mobil yang melaju dijalan raya akan mendapatkan percepatan yang sebanding dengan gaya dan berbading terbalik.

5. kita mendorong gerobak yang penuh dengan batu bata, untuk dipindahkan kerumah.

Contoh Gerak GLB

5 contoh gerak


# . GLB
1 . kecepatan tetap
2 . gerak rotasi bumi
3 . perputaran jarum jam
4 . kendaraan yang melintasi jalan tol
5 . kereta api diatas rel

# . GLBB
1 . mobil melaju dengan kecepatan berubah ubah
2 . gerak jatuhnya buah kelantai
3 . pena menggelinding dari tempat yang tinggi
4 . motor yang bergerak dari lampu merah
5 . kereta bergerak dari stasiun

# . Gerak Lurus Vertikal Kebawah
1 . buah kelapa jatu dari pohonnya
2 . pena jatuh dari atas meja belajar
3 . air hujan jatuh dari langit
4 . salju jatuh dari atas langit
5 . bola dilempar keatas kemudian jatuh 

ulangan matematika XTKJ2

1. X+5 =15
2. 28 =X-35
3. -3X+X =13
4. 5 =2X+25
5. 8X-3 =11+10x
6. -8X+35 =2X+15
7. 2(5+4X)8X =58
8. 
   
9. 8Z-14 =-62
10. 3X-5 =-X+35

Jawab :

1. X+5 =15

    X =15-5

    X =10

2. X =X-35

    28+35 =X

    63 =X

3. -3X+X =13

    -4X =13

       X =13:4

       X =3,25

4. 5 =-2X+25

    5+25 =-2X

        30 =-2X

    30:-2 =X

          X =15

5. 8X-3 =11+10X

    8X-10X =11+3

           -2X =14

              X =14:2

              X =6

6. -8X+35 =2X+15

    -8X+2X =35-15

           -10X =50

                X =50:-10

                X =5

7. 2(5+4X)+8 =58

8.TIDAK ADA SOAL

9. 8Z-14 =-62

          8Z =-62+14

            Z =-74:8 =9

10. 3X-5  =-X+35

      3X-X =35-5

           3X=30

             X= 30:3

             X= 10

Fosil Manusia Tertua

Tim arkeolog dari Universitas Tel Aviv menemukan fosil manusia tertua di dunia yang diperkirakan berusia 400.000 tahun. Fosil terdiri dari delapan buah gigi tersebut sebenarnya sudah ditemukan pada 2006, namun analisa untuk mengetahui umurnya baru dilakukan tahun ini. Fosil gigi tersebut ditemukan di Gua Qesem, Rosh Ha'Ayin, Israel.

"Satu gigi ditemukan di lapisan gua yang kira-kira sudah berusia 400.000 tahun, sementara gigi lain ditemukan di bagian yang usianya kurang lebih 200.000 tahun," papar Avi Gopher, pimpinan penelitian ini.

Menurut Gopher, fosil gigi ini merupakan fosil Homo Sapiens yang pernah ada. Usia 400.000 tahun yang dimiliki fosil gigi ini mengalahkan fosil dari Afrika berusia 200.000 tahun, yaitu fosil yang selama ini dipercaya fosil tertua. Dilihat dari umurnya, diperkirakan fosil gigi tersebut berasal dari zaman Pleistocene Tengah.

Penemuan ini, kata Gopher, bisa membuka pertanyaan baru tentang asal-usul umat manusia. Dengan hasil penelitian ini, manusia bisa jadi bukan berkembang dari Afrika seperti yang selama ini dikenal sebagai teori "Out of Africa", tetapi berkembang dari Timur Tengah, tempat fosil gigi ini ditemukan.

Hasil penemuan dan analisis umur fosil gigi ini kemudian dipublikasikan di American Journal of Physical Anthropology. Saat ini, penggalian di Gua Qesem terus dilakukan.

"Ini berfungsi untuk menguak temuan tambahan lain yang bisa mengkonfirmasi temuan saat ini dan memahami evolusi manusia," kata Gopher.

Bersama fosil tulang gigi ini, lanjut dia, ditemukan pula serpihan peralatan batu yang digunakan untuk memotong daging dan peralatan lainnya. Temuannya menjadi bukti hubungan sosial manusia saat itu yang sudah mengenal perburuan, kebiasaan memotong dan membagi daging hewan serta pembuatan api

Contoh Soal Massa Jenis

Konversi Satuan
Panjang
100 cm = 1 m
1 cm = 0,01 m
80 cm = 80 : 100 = 0,8 m

Massa
1000 gram = 1 kg
1 gram = 0,001 kg
500 gram = 500 : 1000 = 0,5 kg

Volume
1 m3 = 1000000 cm3
1 cm 3 = 0,000001 m3

Massa Jenis
1 g/cm3 = 1 x 0,001/0,000001 = 1000 kg/m3

Konversi Satuan Massa Jenis dengan Cepat

Dari g/cm3 ke kg/m3 → kalikan 1000 Dari kg/m3 ke g/cm3 → bagi 1000

Contoh konversi massa jenis dengan cepat:
0,7 g/cm3 = 0,7 x 1000 = 700 kg/m3
1,2 g/cm3 = 1,2 x 1000 = 1200 kg/m3
1500 kg/m3 = 1500 : 1000 = 1,5 g/cm3
400 kg/m3 = 400 : 1000 = 0,4 g/cm3

Contoh konversi massa jenis dengan satu persatu:
0,7 g/cm3 = 0,7 x 0,001/0,000001 = 0,7 x 1000 = 700 kg/m3
1,2 g/cm3 = 1,2 x 0,001/0,000001 = 1,2 x 1000 = 1200 kg/m3
1500 kg/m3 = 1500 x 1000/1000 000 = 1500 000 / 1000 000 = 1,5 g/cm3
400 kg/m3 = 400 x 1000/1000 000 = 400 000 / 1000 000 = 0,4 g/cm3

Soal No. 1
Sebuah benda bermassa 300 g memiliki volume sebesar 400 cm3. Tentukan massa jenis benda, nyatakan jawaban dalam kg/m3!

Alternatif Jawaban
Data dari soal:
massa benda m = 300 g
volume benda V = 400 cm3

Dengan demikian massa jenis benda :
ρ = m/V = 300 / 400 = 0,75 g/cm3
ρ = 0,75 x 1000 = 750 kg/m3
Thanks to Nida Nur Fitria untuk masukannya ,...

Soal No. 2
Sebuah benda memiliki massa jenis 800 kg/m3 memiliki massa sebesar 2 kg. Tentukan volume benda nyatakan dalam cm3 dan dalam liter!

Alternatif Jawaban
Data dari soal:
massa benda m = 2 kg
massa jenis benda ρ = 800 kg/m3

Dengan demikian volume benda :
V = m / ρ 
V = 2 / 800 m3
V = (2/800) x 1000000 cm3 = 2500 cm3
Dalam satuan liter:
V = 2500 cm3 = 2,5 dm3 = 2,5 liter

Soal No. 3
Balok di bawah memiliki panjang, lebar dan tinggi berturut-turut 20 cm, 5 cm dan 6 cm. Tentukan massa balok jika diketahui massa jenis balok adalah 0,8 g/cm3!


Alternatif Jawaban
Mencari volume benda terlebih dahulu:
V = p x l x t = 20 cm x 5 cm x 6 cm = 600 cm3
Massa balok m = ρ x V = 0,8 x 600 = 480 gram

Soal No. 4
Percobaan untuk memperkirakan massa jenis benda dengan gelas berpancuran yang berisi air.


Jika massa benda telah diketahui sebesar 300 gram, tentukan massa jenis benda!

Alternatif Jawaban
Data:
Volume benda V = 300 ml = 300 cm 3 (terlihat dari gelas ukur)
Massa benda m = 300 gram
Dengan demikian:
ρ = m / V = 300 / 300 = 1 g/cm3

Catatan:
1 ml = 1 cc = 1 cm3

Soal No. 5
Seorang siswa memasukkan benda kedalam gelas ukur. Jika massa benda adalah 300 gram, tentukan massa jenis benda!


Alternatif Jawaban
m = 300 gram
V = 500 − 300 = 200 ml = 200 cm3
ρ = m / V
ρ = 300 / 200 = 1,5 g/cm3

Soal No. 6
Percobaan berikut dilakukan untuk memperkirakan massa jenis suatu benda, setelah ditimbang, benda dimasukkan ke dalam gelas ukur. Tentukan massa jenis benda tersebut!


Alternatif Jawaban
Dari hasil penimbangan diketahui massa benda m = 250 gram
Dari gelas ukur diketahui volume benda adalah V = 500 − 300 = 200 ml = 200 cm3
Dengan demikian massa jenis benda tersebut:
ρ = m / V
ρ = 250 / 200 = 1,25 g/cm3

Soal No. 7
Kubus A bermassa 36 kg dan balok B bermassa 12 kg dengan ukuran masing-masing terlihat pada gambar berikut ini.



Jika kubus dan balok terbuat dari bahan yang sama, tentukan tinggi balok B!

Pembahasan
Kubus dan balok terbuat dari bahan yang sama sehingga keduanya memiliki massa jenis yang sama pula. Sehingga



Soal No. 8
Volum sebuah benda 8 cm3 ditimbang massanya 84 gram, maka massa jenisnya adalah...
A. 10,5 gr/cm3
B. 8,5 gr/cm3
C. 6,4 gr/cm3
D. 4,8 gr/cm3
(Soal Ebtanas SMP 2002)

Pembahasan
Data benda
m = 84 gram
V = 8 cm3
ρ = ....

ρ = m / V
ρ = 84 / 8 = 10,5 gr/cm3

Soal No. 9
Sebuah kubus kayu memiliki volume 5 cm3. Jika massa jenis kayu 250 g/cm3, maka massa kayu tersebut...
A. 1250 g
B. 50 g
C. 10 g
D. 2 g
(Soal Ebtanas 2003)

Pembahasan
Data benda
V = 5 cm3
ρ = 250 g/cm3
m = ....

m = ρ × V
m = 250 × 5 = 1250 gram

Soal No. 10
Data massa jenis beberapa bahan logam diberikan pada tabel berikut:

Logam	Massa Jenis (kg/m3)
Aluminium	2.700
Besi	7.900
Kuningan	8.400
Perak	10.500
Emas	19.300
Platina	21.450

Budi memiliki 4 batang logam dengan ukuran yang sama masing-masing volumenya 50 cm3.



Batang logam yang terbuat dari emas murni adalah....
A. (I)
B. (II)
C. (III)
D. (IV)

Pembahasan
Batang (I) → ρ = m / V = 135 / 50 = 2,7 g/cm3
Batang (II) → ρ = m / V = 525 / 50 = 10,5 g/cm3
Batang (III) → ρ = m / V = 395 / 50 = 7,9 g/cm3
Batang (IV) → ρ = m / V = 965 / 50 = 19,3 g/cm3

Cocokkan dengan data tabel, yang terbuat dari emas adalah batang IV.

Contoh Massa Jenis Material

Material	ρ dalam kg/m3	Catatan
Medium antarbintang	10-25 − 10-15	Assuming 90% H, 10% He; variable T
Atmosfer Bumi	1.2	Pada permukaan laut
Aerogel	1 − 2
Styrofom	30 − 120
Gabus	220 − 260
Air	1000	Pada kondisi standar untuk suhu dan tekanan
Plastik	850 − 1400	Untuk polipropilena dan PETE/PVC
Bumi	5515.3	Rata-rata keseluruhan
Tembaga	8920 − 8960	Mendekati suhu ruangan
Timah	11340	Mendekati suhu ruangan
Inti PerutBumi	~13000	Seperti yang tercantum dalam bumi
Urainuma	19100	Mendekati suhu ruangan
Iridium	22500	Mendekati suhu ruangan
Inti matahari	~150000
Inti Atom	~3 × 1017	Seperti yang tercantum dalam neutron star
Bintang neutron	8.4 × 1016 − 1 × 1018
Black hole	4 × 1017	Mean density inside the Schwarzschild radius of an earth-mass black hole (theoretical)

Massa Jenis

Massa Jenis tidak tergantung pada jumlah benda. Apabila jenisnya sama maka nilai massa jenisnya juga sama. Misalnya, setetes air dan seember air mempunyai nilai massa jenis sama yaitu 1 gram/cm^3. Berbagai logam memiliki nilai Massa Jenis besar dikarenakan atom-atom dalam susunan molekulnya memiliki kerapatan yang besar. Gabus atau sterofoam mempunyai Massa Jenis kecil karena susunan atom-atom dalam molekulnya memiliki kerapatan kecil.

Massa jenis dilambangkan dengan simbol ρ (dibaca rho), salah satu huruf Yunani.

Keterangan:

ρ = Massa Jenis (kg/m^3 atau g/cm^3)

m = massa benda (kg atau gram)

V = volume benda m^3 atau cm^3)

Tabel berbagai Massa Jenis zat

Dari tabel tersebut dapat diketahui bahwa kerapatan logam tertentu seperti platina atau emas jauh lebih besar dibandingkan zat-zat lainnya. Massa jenis berbagai zat berbeda-beda walaupun benda-benda tersebut jumlah atau volumenya sama. Massa Jenis zat yang umum digunakan sebagai patokan adalah Massa Jenis air danMassa Jenis raksa. Massa Jenis air dalam wujud cair, yaitu 1000 kg/m^3 atau 1 g/cm^3, sedangkan raksa atau mercury memiliki Massa Jenis 13.600 kg/m^3 atau 13,6 g/cm^3.

Penting: 1000 kg/m^3 = 1 g/cm^3


Selain massa jenis, dikenal pula berat jenis. Berat jenis adalah berat benda (w) tiap satuan volume (V). Bila berat jenis dapat dilambangkan dengan S, dapat dinyatakan dengan persamaan

Keterangan:

S = berat jenis (N/m^3 atau dyne/cm^3)

w = berat benda (N atau dyne)

V = volume benda (m^3 atau cm^3)

 

Jadi, berat jenis benda adalah hasil kali antara Massa Jenis dengan percepatan gravitasi.

Penggunaan Konsep Massa Jenis dalam Kehidupan Sehari-Hari

Kapal Selam

Tahukah kamu mengapa es dapat terapung di air, sedangkan batu tenggelam dalam air? Es memiliki Massa Jenis lebih kecil dari air, sehingga es dapat terapung dalam air. Batu tenggelam dalam air karena memiliki massa jenis lebih besar daripada air. Tahukah kamu mengapa kapal selam dapat terapung dan tenggelam di air? Ketika terapung Massa Jenis total kapal selam lebih kecil dari air laut dan sewaktu tenggelam Massa Jenis total kapal selam lebih besar dari air laut. Kapal selam memiliki tangki pemberat yang berisi air dan udara. Tangki tersebut terletak di antara lambung kapal sebelah dalam dan luar. Tangki dapat berfungsi membesar atau memperkecilMassa Jenis total kapal selam. Ketika air laut dipompa masuk ke dalam tangki pemberat, Massa Jenis kapal selam lebih besar dan sebaliknya agar Massa Jenis total kapal selam menjadi kecil, air laut dipompa keluar.


Balon Gas 
Pernahkah kamu melihat balon udara? Tahukah kamu, gas apa yang terdapat di dalamnya? Balon gas berisi gas helium. Gas helium memiliki Massa Jenis yang lebih kecil dari udara, sehingga balon gas bisa naik ke atas.


Air Minum Dingin di Dalam Lemari Es
Suatu ketika kamu mungkin pernah melihat dalam botol air minum dingin yang berasal dari lemari es terdapat endapan kapur. Kenapa hal itu dapat terjadi? Air yang jernih dapat juga mengandung kapur, namun apabila dilihat langsung dengan mata tidak kelihatan. Ketika air dingin massa jenis air lebih kecil dan terpisah dari kapur sehingga kapur yang memiliki Massa Jenis lebih besar akan turun ke bawah dan mengendap.

 

 

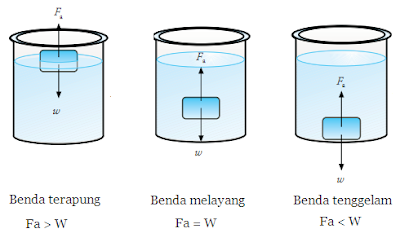
Menganalisis Benda Terapung, Melayang, Dan Tenggelam

Dengan membandingkan Massa Jenis zat cair dan benda yang dicelupkan kedalamnya, kamu dapat mengetahui benda-benda tersebut terapung melayang, atau tenggelam.

Teknik Pemograman Pada halaman web

Teknik Pemograman Pada Halaman Web

Pemrograman web diambil dari 2 suku kata yaitu pemrograman dan web. Pemrograman diartikan proses, cara, perbuatan program. Definisi Web : jaringan komputer yang terdiri dari kumpulan situs internet yang menawarkan teks dan grafik dan suara dan sumber daya animasi melalui protokol transfer hypertext. Orang banyak mengenal web dengan istilah WWW (world wide web), World Wide Web adalah layanan internet yang paling populer saat ini internet mulai dikenal dan digunakan secara luas setelah adanya layanan WWW. WWW adalah halaman-halaman website yang dapat saling terkoneksi satu dengan lainnya (hyperlink) yang membentuk samudra belantara informasi. WWW berjalan dengan protokol HyperText Transfer Protokol (HTTP). Halaman Web merupakan file teks murni (plain text) yang berisi sintaks-sintaks HTML yang dapat dibuka/ dilihat/ diterjemahkan dengan Internet Browser . Sintaks HTML mampu memuat konten text, gambar, audio, video dan animasi. Kini internet identik dengan web, karena kepopuleran web sebagai standar interface pada lanyanan-layanan yang ada di internet, dari awalnya sebagai penyedia informasi, ini digunakan juga untuk komunikasi dari email sampai dengan chatting, sampai dengan melakukan transaksi bisnis (commerce)

Banyak keuntungan yang diberikan oleh Aplikasi berbasis Web dari pada aplikasi berbasis desktop, sehingga aplikasi berbasis web telah diadopsi oleh perusahaan sebagai bagian dari strategi teknologi informasinya, karena beberapa alasan :

1.   Akses informasi mudah,

2.   Setup server lebih mudah

3.   Informasi mudah didistribusikan

4.   Bebas platform, informasi dapat disajikan oleh browser web pada sistem operasi mana saja karena adanya standar dokumen berbagai tipe data dapat disajikan

Format teks pada halaman web

Format Teks Pada Halaman Web

MATERI:
Struktur dasar dokumen HTML(Tag, Element, Attribute), Element HTML, Element HEAD, Element TITLE, Element BODY.

STRUKTUR DASAR DOKUMEN HTML
HTML merupakan singkatan dari HyperText Markup Language adalah script untuk menyusun dokumen-dokumen Web. Dokumen HTML disimpan dalam format teks reguler dan mengandung tag-tag yang memerintahkan web browser untuk mengeksekusi perintah-perintah yang dispesifikasikan.

Struktur dasar dokumen HTML adalah sebagai berikut:

<html> <head> <title>Disini Judul Dokumen HTML</title> </head> <body>  Disini penulisan informasi Web </body> </html>

Dari struktur dasar HTML di atas dapat dijelaskan sebagai berikut:

A.    Tag
Adalah teks khusus (markup) berupa dua karakter “<” dan “>“,  sebagai contoh <body> adalah tag.dengan nama body.
Secara umum tag ditulis secara berpasangan, yang terdiri atas tag pembuka dan tag penutup (ditambahkan karakter “/” setelah karakter “<“), sebagai contoh <body> ini adalah tag pembuka isi dokumen HTML, dan </body> ini adalah tag penutup isi dokumen HTML.

B.    element        
Element terdiri atas tiga bagian, yaitu tag pembuka, isi, dan tag penutup. Sebagai contoh untuk menampilkan judul dokumen HTML pada web browser digunakan element title, dimana:

<title> ini adalah tag pembuka judul dokumen HTML
Disini Judul Dokumen HTML ini adalah isi judul dokumen HTML
</title> ini adalah tag penutup judul dokumen HTML

Tag-tag yang ditulis secara berpasangan pada suatu element HTML,  tidak boleh saling tumpang tindih dengan pasangan tag-tag lainnya.
Contoh penulisan tag-tag yang benar

<p> <b>  ……………. </b> </p>

Contoh penulisan tag-tag yang salah

<p> <b>  …………….  </p> </b>

C. Attribute
Attribute mendefinisikan property dari suatu element HTML, yang terdiri atas nama dan nilai. Penulisannya adalah sebagai berikut:

<TAG nama-attr=”nilai-attr” nama-attr=”nilai-attr” …………….. >    ……………..</TAG>

Secara umum nilai attribute harus berada dalam tanda petik satu atau dua. Sebagai contoh, untuk membuat warna teks menjadi kuning dan latarbelakang halaman web menjadi hitam, penulisannya adalah <body bgcolor=”black” text=”yellow”>

D. Element HTML
Menyatakan pada browser bahwa dokumen Web yang digunakan adalah HTML.

Sintaks:
<html>
……….
</html>

E. Element HEAD
Merupakan kepala dari dokumen HTML. Tag <head> dan tag </head> terletak di antara tag <html> dan tag </html>.

Sintaks:
<head>
………..
</head>

F. Element TITLE
Merupakan judul dari dokumen HTML yang ditampilkan pada judul jendela browser. Tag <title> dan tag </title> terletak di antara tag <head> dan tag </head>.

Sintaks:
<title>
………
</title>

G. Element BODY
Element ini untuk menampilkan isi dokumen HTML. Tag <body> dan tag </body> terletak di bawah tag <head> dan tag </head>.
Element BODY mempunyai attribute-attribute yang menspesifikasikan khususnya warna dan latarbelakang dokumen yang akan ditampilkan pada browser.

Sintaks:
<body text=”v” bgcolor=”w” background=”uri” link=”x” alink=”y” vlink=”z”>
…………..
</body>

Attribute text memberikan warna pada teks, bgcolor memberikan warna pada latarbelakang dokumen HTML, background memberikan latarbelakang dokumen HTML dalam bentuk gambar, link memberikan nilai warna untuk link, alink memberikan warna untuk link yang sedang aktif, vlink memberikan warna untuk link yang telah dikunjungi.
Jika attribute bgcolor dan background keduanya dispesifikasikan maka attribute background yang akan digunakan, akan tetapi jika nilai attribute background (gambar) tidak ditemukan pada dokumen HTML maka attribute bgcolor yang akan digunakan.

Tugas Matematika - Bilangan berpangkat

A. Bilangan Berpangkat Bilangan Bulat

Setiap manusia yang hidup pasti dia akan membutuhkan sesuatu atas dirinya seperti makan, bernafas, pakaian, tempat tinggal, dan lain-lain. Kebutuhan-kebutuhan manusia sebagian besar diperoleh tidak dengan cuma-cuma. Diperlukan sebuah usaha untuk mendapatkannya baik mencari, membeli, dan usaha-usaha yang lainnya.
Untuk membeli sebuah kebutuhan, kadang manusia harus mengeluarkan uang dalam jumlah besar. Misal untuk membeli rumah mewah manusia harus mengeluarkan uang sebesar 1 milyar rupiah. Jika dalam matematika 1 milyar dapat dituliskan dengan 1.000.000.000. Agaknya untuk menuliskan jumlah tersebut terlalu panjang, dapat juga dituliskan dalam bentuk baku yaitu 1 × 109. Nah, bilangan yang dituliskan sebagai 109 inilah yang disebut sebagai bilangan berpangkat. Dalam hal ini 10 disebut bilangan pokok, sedangkan 9 disebut bilangan pangkat. Karena pangkatnya bilangan bulat, maka disebut bilangan berpangkat bilangan bulat.

1. Bilangan Berpangkat Sederhana

Dalam kehidupan sehari-hari kita sering menemui perkalian bilangan-bilangan dengan faktor-faktor yang sama. Misalkan kita temui perkalian bilangan-bilangan sebagai berikut.

Perkalian bilangan-bilangan dengan faktor-faktor yang sama seperti di atas, disebut sebagai perkalian berulang. Setiap perkalian berulang dapat dituliskan secara ringkas dengan menggunakan notasi bilangan berpangkat. Perkalian bilanganbilangan di atas dapat kita tuliskan dengan:

Bilangan 2³, 3⁵, 6⁶ disebut bilangan berpangkat sebenarnya karena bilangan-bilangan tersebut dapat dinyatakan dalam bentuk perkalian berulang. Bilangan berpangkat aⁿ dengan n bilangan bulat positif didefinisikan sebagai berikut.

3. Bilangan Berpangkat Negatif

Apa yang terjadi jika m = 0? Dari pembahasan di atas jika dipilih m = 0, maka:

B. Bilangan Pecahan Berpangkat

Untuk menentukan hasil pemangkatan bilangan pecahan berpangkat dapat di gunakan definisi bilangan berpangkat. Jika a, b∈ B, b ≠ 0, n adalah bilangan bulat positif maka:

C. Bentuk Akar

Dalam matematika kita mengenal berbagai jenis bilangan. Beberapa contoh jenis bilangan diantaranya adalah bilangan rasional dan irrasional. Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk , dengan m, n ∈ B dan n ≠ 0. Contoh bilangan rasional seperti: , 5, 3 dan seterusnya. Sedangkan bilangan irrasional adalah bilangan riil yang tidak dapat dinyatakan dalam bentuk , dengan m, n ∈ B dan n ≠ 0. Bilangan-bilangan seperti termasuk bilangan irrasional, karena hasil akar dari bilangan tersebut bukan merupakan bilangan rasional.
Bilangan-bilangan semacam itu disebut bentuk akar. Sehingga dapat disimpulkan bahwa bentuk akar adalah akar-akar dari suatu bilangan riil positif, yang hasilnya merupakan bilangan irrasional.

1. Operasi Hitung Bentuk Akar

Dua bilangan bentuk akar atau lebih dapat dijumlahkan, dikurangkan, maupun dikalikan.

A. Penjumlahan dan Pengurangan Bentuk Akar

Untuk memahami cara menjumlahkan dan mengurangkan bilangan-bilangan dalam bentuk akar, perhatikan contoh - contoh berikut.

Dari contoh di atas, maka untuk menjumlahkan dan mengurangkan bilangan-bilangan dalam bentuk akar dapat dirumuskan sebagai berikut. Untuk setiap a, b, dan c bilangan rasional positif, berlaku hubungan:

B. Perkalian Bentuk Akar

Untuk sembarang bilangan bulat positif a dan b berlaku sifat perkalian berikut.

Sifat di atas sekaligus dapat digunakan untuk menyederhanakan bentuk akar.

C. Pemangkatan Bilangan Bentuk Akar

Bentuk akar juga dapat dipangkatkan. Adapun pemangtkatan bentuk akar akar didapat beberapa sifat.

2) Pemangkatan bentuk dengan pangkat negatif
Bentuk akar dengan pangkat negatif sama halnya dengan bilangan berpangkat bilangan negatif. Sehingga:

2. Hubungan Bentuk Akar dengan Pangkat Pecahan

Pada pembahasan yang lalu telah disebutkan beberapa sifat dari bilangan berpangkat bulat positif. Sifat-sifat tersebut akan digunakan untuk mencari hubungan antara bentuk akar dengan pangkat pecahan. Sifat yang dimaksud adalah .

Selain sifat tersebut terdapat sifat lain, yaitu:Jika ap = aq maka p = q dengan a > 0, a ≠ 1

a. Hubungan dengan

Perhatikan pembahasan berikut.

Dari uraian di atas dapat disimpulkan bahwa untuk a bilangan real tidak nol dan n bilangan bulat positif, maka:

D. Merasionalkan Bentuk Akar Kuadrat

Dalam sebuah bilangan pecahan penyebutnya dapat berupa bentuk akar. Pecahan adalah beberapa contoh pecahan yang penyebutnya berbentuk akar. Penyebut pecahan seperti itu dapat dirasionalkan. Cara merasionalkan penyebut suatu pecahan tergantung dari bentuk pecahan tersebut.

1. Merasionalkan Bentuk

Untuk menghitung nilai ada cara yang lebih mudah daripada harus membagi 6 dengan nilai pendekatan dari 3, yaitu dengan merasionalkan penyebut. Cara ini dapat dilakukan dengan menggunakan sifat perkalian bentuk akar:

Selanjutnya pecahan diubah bentuknya dengan memanipulasi aljabar.

2. Merasionalkan Bentuk